9. Discrete time Kermack-McKendrick Model

Why does the SIR assume an exponential distribution for the infectious period?

The majority of work with compartmental models assumes that the amound of time an individual spends in a disease state is exponentially distributed. For example, for the SIR model

(9.1)\[\begin{align} \frac{dS}{dt} &= -\beta \frac{SI}{N} \\ \frac{dI}{dt} &= \beta \frac{SI}{N} - \gamma I \\ \frac{dR}{dt} &= \gamma I \end{align}\]

after an individual becomes infectious (moves from S to I) they spend on average \(1/\gamma\) time units in this infectious state. However, we may wonder what the density of infectious periods (time spend in the I state) is. The SIR model implicitly assumes that the density of infectious periods is exponential. To see this, for a small increment of time \(\tau\), we assume an individual leaves the infectious state with probability \(\gamma \tau\). This means that an individual remains infectious for this small period of time \(\tau\) with probability \(1-\gamma \tau\). Then the probability that an individual is still infectious in the interval \(t + \tau\) is the probability that they remain infectious in the interval \([0,\tau],[\tau,2\tau],[2\tau,3\tau],\cdots,[t-\tau ,t]\) equals \(p(\text{still infectious}) = (1-\gamma \tau)^{t/\tau}\) and so the probability that they are no longer infectious in the interval \([t,t+\tau]\) is

(9.2)\[\begin{align} p( \text{no longer infectious} \in [t,t+\tau] ) = \gamma \tau (1-\gamma \tau)^{t/\tau} \end{align}\]

For continuous time, when \(\tau\) moves towards infinity, from calculus we know that

(9.3)\[\begin{align} \lim_{\tau \to 0} (1-\gamma \tau)^{t/\tau} = e^{-\gamma t} \end{align}\]

we also know that in continuous time, as we shrink this interval \(\tau\), that probabilities turn into probability densities. In other words

(9.4)\[\begin{align} p( \text{no longer infectious} \in [t,t+\tau] ) \approx f(t) \tau \end{align}\]

where \(f\) is the probability density that an individual is no longer infectious in an interval from \(t\) to \(t+\tau\). Then as \(\tau\) shrinks we find that

(9.5)\[\begin{align} p( \text{no longer infectious} \in [t,t+\tau] ) &= \gamma \tau (1-\gamma \tau)^{t/\tau} \\ f(t) \tau &\approx \gamma \tau e^{-\gamma t} \\ f(t) &= \gamma e^{-\gamma t} \end{align}\]

The density above \(f(t)\) is an exponential distribution with paramter \(\gamma\).

The derivative of the above is

(9.6)\[\begin{align} \frac{df}{dt} = -\gamma \left[\gamma e^{-\gamma t}\right] = -\gamma f(t) \end{align}\]

This is the key. We assume in the SIR model that infectious individuals leave the infectious state like

(9.7)\[\begin{align} \frac{dI}{dt} = -\gamma I \end{align}\]

This can only mean that the infectious period is assumed to have an exponential density.

The discrete-time Kermack McKendrick model

If an infectious diseases did have an exponential period then it would mean that the probability you remain infectious decreases tremendously with time and that there is no ‘typical’ time in which an individual is infecitous. For most infectious diseases, an exponential distributed infectious period is unrealistic because there is a typical amount of time an individual remains infectious.

Our goal will be to study the discrete-time Kermack McKendrick model as a means of incorporating any type of infectious period. We will follow closely the paper: The discrete-time Kermack–McKendrick model: A versatile and computationally attractive framework for modeling epidemics.

For the typical SIR, we assume that the number of susceptibles is depleted like

(9.8)\[\begin{align} \frac{dS(t)}{dt} = -\beta \frac{I(t)}{N} S(t) \end{align}\]

We can think of \(\beta \frac{I(t)}{N}\) as a function of the number of infectors in the system. This function is often called the force of infection and, for the SIR model, is defined as the function \(\Lambda(t)\) of \(t\)

(9.9)\[\begin{align} \Lambda(t) = \beta \frac{I(t)}{N} \end{align}\]

We can substitute in the above function to obtain

(9.10)\[\begin{align} \frac{dS(t)}{dt} = - \Lambda(t) S(t) \end{align}\]

However the function that we chose, \(\Lambda(t) = \beta \frac{I(t)}{N}\) , is just one of an infinite number of force of infection functions that we can use to describe the loss of susceptibles to infections. For now, lets continue with the general function \(\Lambda(t)\). Suppose we wish to solve the above differential equation over a small time interval from \(t\) to \(t+\tau\). The fundemental theorem of calculus tell us to integrate

(9.11)\[\begin{align} \int_{x=t}^{x=t+\tau} \frac{dS(x)}{dx} \frac{1}{S(x)} \; dx = - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \\ \int_{x=t}^{x=t+\tau} \frac{ d \left[\log(S(x))\right]}{dx} \; dx = - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \\ \log(S(t+\tau)) - \log(S(t)) = - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \\ \log\left[ \frac{S(t+\tau)}{S(t)} \right] = - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \\ \frac{S(t+\tau)}{S(t)} = \exp \left[ - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \right]\\ S(t+\tau) = S(t)\exp \left[ - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \right] \end{align}\]

Lets simplify the above equation by defining the cumulative force of infection

(9.12)\[\begin{align} \hat{\Lambda} (t) = \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \end{align}\]

Then our final equation above simplifies to

(9.13)\[\begin{align} S(t+\tau) &= S(t)\exp \left[ - \int_{x=t}^{x=t+\tau} \Lambda(x) \; dx \right] \\ &= S(t)\exp \left[- \hat{\Lambda} (t)\right] \\ \end{align}\]

Note: that the number of susceptibles can only stay the same or decrease because the expression \(\exp \left[- \hat{\Lambda} (t)\right]\) is at most the value one. That is, for this formulation, we do not consider individuals moving back to the susceptible disease state.

Though we can use any function \(\hat{\Lambda} (t)\), a common function supposes that previously infected individuals can infect others in the system. This is the defining characteristic of an infectious diseases—that the risk of disease is related to the number of infections in the system.

The original 1927 paper that specifies the evolution of an infectious disease chose as a function

(9.14)\[\begin{align} \hat{\Lambda}(t) = \int_{l=0}^{l=\infty} \mathcal{A}(l) \times \Lambda(t-l) S(t-l) \; dl \end{align}\]

where we say that \(l\) is the lag or a number that describes the number of time units in the past (relative to \(t\)). This proposed function has two components. The function \(\mathcal{A}(l)\) needs to be set by the modeler as is called the contribution to the force of infection. More on this later. The term \(\Lambda(t-l) S(t-l)\) is the change in the number of susceptibles \(l\) time units ago. For the Kermack-McKendrick model, all the susceptibles move to the infected state. That is, the change in the number of susceptibles is the number of incident infections at time \(t-l\).

Define incident infections at time \(t\). Then

(9.15)\[\begin{align} \hat{\Lambda}(t) = \int_{l=0}^{l=\infty} \mathcal{A}(l) \times i(t-l)\; dl \end{align}\]

The contribution to the force of infection should be interpreted as the probability that an infected individual makes effective contact, contact resulting in infection, when they come into contact with a susceptible.

An equation for the basic reproduction number

Suppose that we introduce a single infected individual at time zero into a population where the remaining \(N-1 \approx N\) individuals are susceptible. Then at time zero this incident, infected individual is expected to contact all \(N\) susceptibles and infect on average \(N \mathcal{A(0)}\) of them. Lets continue to follow the path of this incident infector. At time one, we would expect that they infect \(N \mathcal{A(1)}\) susceptibles (assuming the population is approximately still \(N\)). At time two, three, and four we would expect this infector to produce \(N \mathcal{A(2)}\),\(N \mathcal{A(3)}\),\(N \mathcal{A(4)}\) infections.

That is, the expected number of infections generated from a single infected individual in an entirely susceptible population is

(9.16)\[\begin{align} \mathcal{R}_{0} = N \int_{l=0}^{l=\infty} \mathcal{A}(l) \; dl \end{align}\]

Discretization to make things a bit easier

We typically do not, and cannot, observe outbreaks on a continuous timescale. Public health resources are limited and so we typically observe incident, reported infections at the day, week, month, or even only the annual time scale. Because of this, it makes more sense to look at a discretized version of the above. That is, to replace integrals with summations.

Our discretized KM model is

(9.17)\[\begin{align} S(t+1) &= S(t) \exp\left[ -\hat{\Lambda}(t) \right] \\ \Lambda(t) &= \sum_{l=0}^{l=C} \mathcal{A}(l) \times i(t-l) \end{align}\]

where we introduce the parameter \(C\) as a limit to how far back we “look” when assuming infectors in the past are generating new infections. That is, we assume an individual who was infected \(C\) time units ago is no longer producing new infections.

The generation interval

Let \(\sum_{l=0}^{\infty} \mathcal{A}(l)\) be the total number of average infections (the basic reproduction number) for a single infector. Then \(g(l) = A(l) / \sum_{l=0}^{\infty} \mathcal{A}(l)\) is the probability that an individual was infected \(l\) time units ago. The time between an infector contacting a susceptible and when that susceptible becomes infectious is called the generation interval.

To see this, suppose

(9.18)\[\begin{align} \mathcal{A}(0) &= 1/2 \\ \mathcal{A}(1) &= 1/4 \\ \mathcal{A}(2) &= 1 \\ \mathcal{A}(3) &= 1/3 \end{align}\]

or we expect a single infector to produce a total of 2.08 infections. Lets normalize the above \(\mathcal{A}\). Then we find

(9.19)\[\begin{align} g(0) &= 0.24 \\ g(1) &= 0.12 \\ g(2) &= 0.48 \\ g(3) &= 0.16 \end{align}\]

and say that there is a (for example) 0.48 probability that 2 time units ago a susceptible individual made effective contact with an infector and is now infectious.

The above argument suggests a relationship between the basic reproduction number, contribution to force of infection, and the generation interval.

(9.20)\[\begin{align} g(l) = \frac{\mathcal{A}(l)}{\mathcal{R}_{0}} \end{align}\]

Coding up the discrete time KM model

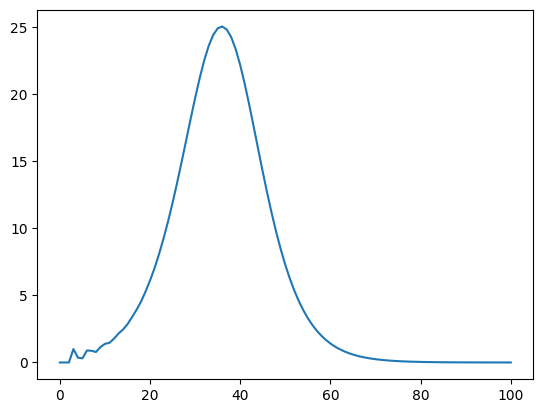
def g(t):
    if t==0:
        return 0.24
    elif t==1:
        return 0.12
    elif t==2:
        return 0.48    
    elif t==3:
        return 0.16
    else:
        return 0 


def A(R0,g,t):
    return R0*g(t)

start,end = 0,100
S0        = 1000
N         = 1001

R0 = 1.50/N

S = [S0]
i = [0,0,0,1]

for t in np.arange(start+3,end):
    #--compute lambda
    L = 0
    for l in np.arange(0,4):
        L = L+A(R0,g,l)*i[t-l]
    St = S[-1]*(np.exp(-L))
    
    i.append( S[-1]-St )
    S.append( St )

i_g1 = i

---------------------------------------------------------------------------
NameError                                 Traceback (most recent call last)
Cell In[1], line 26
     23 S = [S0]
     24 i = [0,0,0,1]
---> 26 for t in np.arange(start+3,end):
     27     #--compute lambda
     28     L = 0
     29     for l in np.arange(0,4):

NameError: name 'np' is not defined

plt.plot(i_g1)

[<matplotlib.lines.Line2D at 0x140aeb0d0>]

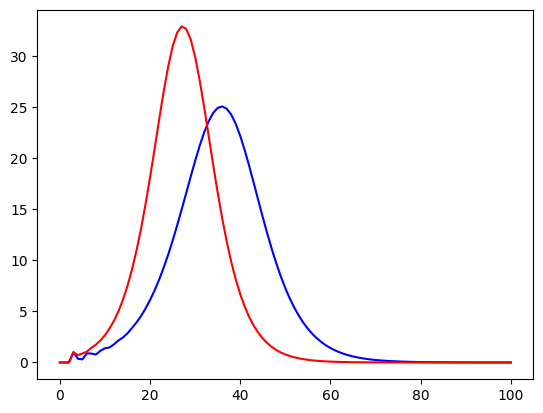
def g(t):
    if t==0:
        return 0.48
    elif t==1:
        return 0.24
    elif t==2:
        return 0.12    
    elif t==3:
        return 0.16
    else:
        return 0 
        
def A(R0,g,t):
    return R0*g(t)

start,end = 0,100
S0        = 1000
N         = 1001

R0 = 1.50/N

S = [S0]
i = [0,0,0,1]

for t in np.arange(start+3,end):
    #--compute lambda
    L = 0
    for l in np.arange(0,4):
        L = L+A(R0,g,l)*i[t-l]
    St = S[-1]*(np.exp(-L))
    
    i.append( S[-1]-St )
    S.append( St )

i_g2 = i

plt.plot(i_g1,color="blue")
plt.plot(i_g2,color="red")
plt.show()

Homework

1. A manuscript in 2009 estimated the generation interval for influenza to be on average 3.6 days with a standard deviation of 1.6 days. Lets assume that the generation interval (a probability mass function) takes the form of a Poisson distribution.

   1. Define a function g that takes as input a lag \(t\) and parameter \(p\) and returns the the generation interval value at that lag computed as Pois(l;\(p\)) where Pois(l;\(p\)) is the Poisson distribution evaluated at l with parameter value \(p\).

   2. A typical reproduction number for influenza is 1.5. Use the generation interval above with parameter \(3.6\) and plot the number of incident infection over time from 0 to 100 time units.

   3. Change the generation interval parameter from \(3.6\) to \(4.6\) and overlay the number of incident infections for (2) as well as for this new parameter value.

   4. Discuss the implications of estimating the generation interval precisely.

2. For the Reed-Frost model, we found that the basic reproduction number was \(Np\). Please use the relationship between the reproduction number and contribution to force of infection to identify the contribution to the force of infection for the Reed-frost model.

3. Lets assume a simple model for how infections propogate, and using this model, understand the relationship between how fast an infecitous disease grows and the reproduction number.

Lets assume that when an individual is infected that they become infectious after \(T_{1}\) time units and stay infectius until \(T_{2}\) time units. For example, we might assume that a susceptible individual who comes into contact with an infector becomes infected 3 days later and stays infected until 8 days after that initial contact (the infectious period is 8-3= 5 days).

Further lets assume that the probability an infector passes the pathogen to a susceptible is \(p\) and that each individual comes into contact with \(c\) individuals. Then at the beginning of an outbreak (everyone they contact is susceptible) the basic reproduction number is

(9.21)\[\begin{align} R_{0} = pc (T_{2}-T_{2}) \end{align}\]

Then we can assume that the number of new infectors \(i(t)\), early in the spread of disease, follows

(9.22)\[\begin{align} i(t) = \int_{\tau=0}^{\tau=\infty} pc \times i(t-\tau) d\tau = \int_{\tau=T_{1}}^{\tau=T_{2}} pc \times i(t-\tau) d\tau \end{align}\]

This can be interpreted as follows: At time \(t\) we will look back at the number of infectors who were infected: 1 day, knowing that they will produce \(pc\) infections each for a total of \(pc \cdot i(t-1)\) infections; 2 days, knowing that each of the \(i(t-2)\) infecors will produce \(pc\) infections for a total of \(pc \cdot i(t-2)\) and so on.

In the beginning of an outbreak, its safe to assume that the growth in the number of infections follows

(9.23)\[\begin{align} i(t) = Ce^{rt} \end{align}\]

for some parameter \(r\)—called the growth rate (or Malthusian parameter).

Lets substitute this assumed exponential growth rate into the above number of incident infection over time.

(9.24)\[\begin{align} i(t) &= \int_{\tau=T_{1}}^{\tau=T_{2}} pc \times i(t-\tau) d\tau \\ e^{rt} &= \int_{\tau=T_{1}}^{\tau=T_{2}} pc \times e^{r(t-\tau)} d\tau \\ 1 &= \int_{\tau=T_{1}}^{\tau=T_{2}} pc \times e^{-r\tau} d\tau \end{align}\]

The above equation is dense, but can tell us a few interesting things. To be clear, the above equation says that if we assume an exponential growth in infections then the growth rate \(r\) is that value such that \(\int_{\tau=T_{1}}^{\tau=T_{2}} pc \times e^{-r\tau} d\tau\) is equal to one.

Lets consider the right hand side a function \(f(r)\) of the grow rate \(r\)—how fast infections are spreading.

(9.25)\[\begin{align} 1 &= f(r; p,c,T_{1},T_{2})\\ \end{align}\]

where we defined the function

(9.26)\[\begin{align} f(r) &= \int_{\tau=T_{1}}^{\tau=T_{2}} pc \times e^{-r\tau} d\tau \\ \end{align}\]

It may be easier to multiply (and divide) by \((T_{2}-T_{1})\) to specify this function in terms of the reproduction number.

(9.27)\[\begin{align} f(r ; R_{0}, T_{2}, T_{1}) &= \frac{1}{T_{2}-T_{1}} \int_{\tau=T_{1}}^{\tau=T_{2}} R_{0} \times e^{-r\tau} d\tau \\ \end{align}\]

To estimate r, the growth rate, we know that given the parameters R_{0}, T_{2}, T_{1} the growth rate r is that value such that f(r)=1 We also know that f(0) = \(R_{0}\).

Question 3a: Please show that \(f(0) = R_{0}\)
Question 3b: Please plot \(f\) values for growth rates from -1 to 1 for the following parameters:
(i) \(R_{0}=0.45; T_{1}=1; T_{2}=5\)
(ii) \(R_{0}=1; T_{1}=1; T_{2}=5\)
(iii) \(R_{0}=2; T_{1}=1; T_{2}=5\)
(iii) \(R_{0}=3; T_{1}=1; T_{2}=5\)

Set the xlimits of your plot to (-1,1) and the ylimits (0,5).
Add a horizontal line at the value 1 and a vertical line at 0.
For the above, what is the relationship between \(R_{0}\) and \(r\)? Hint: Use the quad function from scipy to help you compute that integral.

Question 3c: Please plot \(f\) values for growth rates from -1 to 1 for the following parameters:
(i) \(R_{0}=2; T_{1}=1; T_{2}=5\)
(ii) \(R_{0}=2; T_{1}=1; T_{2}=10\)
(iii) \(R_{0}=2; T_{1}=1; T_{2}=50\)

Set the xlimits of your plot to (-1,1) and the ylimits (0,5).
Add a horizontal line at the value 1 and a vertical line at 0.
For the above, what is the relationship between \(R_{0}\) and the infectious period ?
Hint: Use the quad function from scipy to help you compute that integral.