1. Chapter One - Reed-Frost dynamics#
Assumptions and setup#
Suppose that there exists \(N\) individuals who can exist in one of three disease states starting at time \(0\) and ending at time \(T\):
Susceptible - An individual is not infected at present but can be infected in the future.
Infected - An individual is infected at present and can infect other susceptible individuals.
Removed - An individual is no longer susceptible, nor infected, and cannot again become infected.
Assume, for each time unit, that all \(N\) individuals come into contact with one another, and that each interaction is independent. When a susceptible comes into contact with an infected, the susceptible individual has a probability \(p\) of moving from the susceptible state to the infected state (\(S \to I\)).
Assume that if an individual is infected then they (1) are only infected for a single time unit and (2) after that time units ends they are removed.
Assume that the probability of infection should depend on the number of infected individuals in the population.
Probability of escape and infection#
Consider a single susceptible individual. At time \(t\), this susceptible individual will contact all \(I\) infected individuals. At each contact between the susceptible individual and one of the infected individuals, there is a probability \(p\) that the infected individual is successful and infects this susceptible individual.
If \(p\) is the probability that an infected individual—often called can infector—can infect this susceptible then the probability that an infector does not infect this susceptible is \(1-p\). Then the probability that this susceptible is not infected by the first member in \(I\) is \((1-p)\) and the probability that this this susceptible is not infected by the first and second infector is
and so the probability that this susceptible is not infected by all infectors in \(I\) is
This is typically called the escape probability.
If \((1-p)^{I}\) is the probability that no infector successfully infects this susceptible then the probability that at least one individual infects this susceptible is
Initial conditions#
The above assumptions and conditions assume that the \(N\) individuals who can exist in one of three disease states may move from one disease state to another over time. Let us be explicit, and define the number of individuals in each disease state at time \(0\), and define how the number of individuals in each of the three disease states is expected to change over time.
The initial conditions assigns a number of individuals to each disease state at time \(0\), and is denoted
where lowercase letters denote an observed or realized number of individuals in each disease state at time \(0\) (the subscript) and lowercase letters with a superscript denote values between \(0\) and \(N\). For this model, the sum of the number of individuals in each disease state must equal \(N\).
Evolution#
Now that we have specified, at time \(0\), the number of individuals who belong to the susceptible disease state (\(s_{0}\)), number of individuals who belong to the infected disease state (\(i_{0}\)), and number of individuals who belong to the removed disease state (\(r_{0}\)), we must decide the number of individuals at the next time step.
At time \(t\), suppose that there exists \(S_{t}\) susceptible individuals. A susceptible individual moves to the infected state with probability \(1 - (1-p)^{I_{t}}\) (see above section on escape). Further, we assume that for each susceptible the probability of moving to the infected state is independent. If we define “success” as \(1 - (1-p)^{I_{t}}\) and the number of trials as \(S_{t}\) then the potential number of infected individuals at time \(t+1\) or \(I_{t+1}\) has a Binomial distribution,
Let the observed number of infected individuals at time \(t+1\) equal \(i_{t+1}\). Then the number of susceptibles at the next time step is then equal to the number of susceptibles at time \(t\) minus the number of susceptibles who became infected.
Finally, we assume that at the end of each time unit all infected individuals at time \(t\) move to the “removed” category. So then,
The Reed Frost Dynamical System#
The system of equations
along with initial conditions
define a system called The Reed Frost Dynamical System. We note that the capital \(I_{t+1}\) indicates that the number of infectors at time \(t+1\) is a random variable. After the number of infectors is determined, the number of susceptibles is automatically determined. However, before the number of infectors is selected the number of susceptibles is itself a random variable.
One should be careful about when the number of susceptibles at time \(t+1\) is a random variable. Before the number of infectors is assigned the number of susceptibles is a random variable. After the number of infectors is assigned then the number of susceptibles is not random.
Simulation#
Below is a simulation of the above Reed Frost Dynamical System. Presented is the number of infected individual at each time unit for a specified number of simulations. At this point, the code (in Python) is not important.
Instead, please select different values for \(p\), the probability of infection; $i^{0} the initial number of infectors; and sims, the number of unique times to run this Reed Frost System.
<function __main__.Reed_Frost_Dynamical_system(sims=10, T=15, N=1000, i0=1, p=0.02, show=True)>
Dynamics assumed at start of outbreak#
At the start of an outbreak, there is a small number of infectors, a large number of susceptible individuals, and (typically) no indiviuals in the removed disease state. One way to represent this state of nature is to assign the following initial conditions \(( s^{0} = N-1, i^{0}=1,r^{0}=0)\).
Given a probability of infection, \(p\), and the above initial conditions, we can explore how the number of infectors changes in the Reed-Frost Dynamical system and how all three disease states behave early during an outbreak (when \(T\) is small).
We know that in the Reed-Frost model,
\(I_{t+1} \sim \text{Bin}(S_{t}, 1-(1-p)^{i_{t}} )\)
Our goal is to understand the behavior of \(I\) when \(t\) is small and when \(i^0\) is small.
First, let \(t=0\). Then
\(I_{1} \sim \text{Bin}(S_{0}, 1-(1-p)^{i_{0}} )\)
In this first time step, the number of initial susceptibles \(s^{0}\) is very close to \(N\) and so
\(I_{1} \sim \text{Bin}(N, 1-(1-p)^{i_{0}} )\)
The above expression for the distribution of the number of infected individuals is not very intuitive. From this equation, we cannot glean any information for how an infection spreads at the start of an outbreak.
Math aside (we need this)#
We want to simplify \((1-p)^{i^{0}}\) to better understand what this expression means. This expression looks a bit like \(x^{a}\). Now the tricks.
Trick 1 The exponential function and logarithm are inverses of one another. That is, we are allowed to take the logarithm of an expression (say \(x\)) followed by the exponential and we will not change the orginal value of our expression.
This means that
Trick 2 An important approximation for the exponential is it’s series expansion.
where \(k!\) is read “k factorial” and equals \(k! = k\cdot(k-1)\cdot(k-2)\cdots 1\). When \(x\) is small, terms like \(x^{2}, x^{3}\) and so on will be so small that they are neglible. In other words, we can approximate
when \(x\) is small.
Trick 3 The logarithm of \(1-x\) is, when \(x\) is small, approximately equal to \(-x\) or
Lets use these three tricks above to approximate \(1-(1-p)^{i_{0}}\) when \(p\) is small.
This means then, when \(p\) is small that
\(I_{1} \sim \text{Bin}(N, 1-(1-p)_{i_{0}} ) \text{ is close to } I_{1} \sim \text{Bin}(N, i_{0}p)\).
The above is an expression for the probability that we observe \(0, 1, 2, \cdots N\) potential number of infectors. To better understand what we may see on average, we can look at the expected value of \(I_{1}\)
This says that, at the start of an outbreak, we expect the number of infectors at the next time step to be approximately \( Np i_{0}\). To understand how the expected number of infectors changes over time we can look at
or the expected number of infectors at \(t=2\) equals the number of animals in the system times the probability of infection and the observed number of infectors at \(t=1\).
When we are at timepoint zero, we have not yet observed the number of infectors at \(t=1\). Instead, lets replace \(i_{1}\) by it’s expected value
and in general
We can check the accuracy of our approximation above—that \(\mathbb{E}\left(I_{t+1}\right) = \left(Np\right)^{t} i_{0}\)—numerically. Below, we plot the number of infectors over time units for 100 separate simulations. We choose a small \(p = 0.0015\) and \(N=1000\) individuals in the system. We also plotted in solid black our approximation.
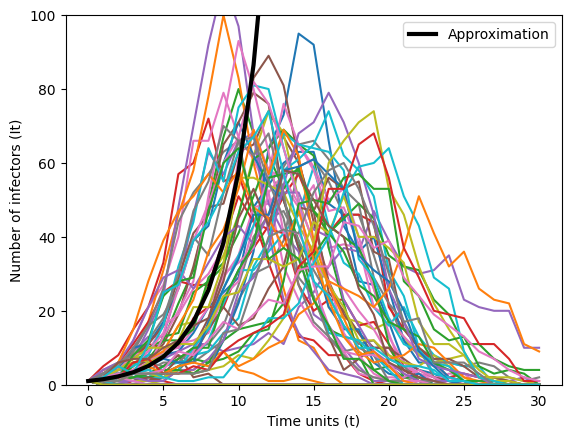
We see that our approximation works well for a small number of time units. After \(t=10\) our approximaton suggests that the number of infectors will continue to increase. However, after time unit 10 the number of infectors begins to decrease towards zero. Note that not all epidemic trajectories fit this approximation.
The Basic Reproduction Number#
Let us observe 100 simulated epidemic trajectories for the above system (plus parameters) for varying values of \(p\). Take a minute to change the parameter value \(p\). What do you observe?
<function __main__.Reed_Frost_Dynamical_system(sims=10, T=15, N=1000, i0=1, p=0.02, show=True)>
After enough trials, you may see that when the value of \(p \ge 1/1000\) that the number of infectors grows to a peak and then declines. For values smaller than \(1/1000\) the infectors never really increase. Instead they decline.
The basic reproduction number is defined as the average number of individuals who move to the infected state as a result of a single infected individual in a population of all susceptibles. For the Reed-Frost Dynamical System, an approximate reproduction number is \(\mathcal{R}_{0} = \mathbb{E}(I_{1}) = Np.\) Intuitively, when a single infector is in the system then they meet all \(\sim N\) susceptible animals and (when \(p\) is small) infect those individuals with probability \(p\).
Relationship between Reproduction number and outbreak#
When infections start to take place, public health officials and epidemiologists typically assign this spread of an infectious agent to one of three classifications: an outbreak, an epidemic, a pandemic. An outbreak is defined as a higher-than-expected number of infections present in a local or small region of space on a short time scale. Like an outbreak, an epidemic is defined as a higher-than-expected number of infections present in an expansive area or among a large community on a short time scale. A pandemic is an outbreak that occurs on a global scale.
Lets look closer at \(\mathbb{E}\left(I_{t+1}\right) = \mathcal{R}_{0}^{t} i_{0}\) If as assume that the number of initial infectors is one, we have
\(\mathbb{E}\left(I_{t+1}\right) = \mathcal{R}_{0}^{t}\)
where \(\mathcal{R}_{0} = Np\) is a constant.
If \(\mathcal{R}_{0} = 1 \) then
and the number of infectos is a constant, never growing one.
If \(\mathcal{R}_{0} < 1 \) then (lets say \(\mathcal{R}_{0}=1/2\))
Finally, If \(\mathcal{R}_{0} > 1 \) then (lets say \(\mathcal{R}=2\))
Intuitively, in order for an infectious agent to continue to spread it must multiply faster than it is removed from the population.
The Effective Reproduction number and Herd Immunity#
The basic reproduction number, \(\mathcal{R}_{0}\), may not always be a realistic way to characterize whether an infecitous agent will begin to spread within a population. This is because the number (or proportion) of susceptibles in the population may not be close to \(N\). For example, if an infectious agent has a \(\mathcal{R}_{0}=3\) then in a fully susceptible population we would expect an infector to infect three susceptibles. However, if the population was immune~(for example vaccinated) to the infectious agent then there are 0 susceptibles. In the case where there are no suscpetibles, the this infecitous agent with \(\mathcal{R}_{0}=3\) would not propogate at all.
To characterize the importance of the proportion of susceptibles on thespread of an infectious agent in the population, we define the effective reproduction number. The Effective reproduction number is the expected number of susceptibles individuals who will get infected at the next time unit. Note, we left out of the above definition the added constraint that the population must be fully susceptible.
For the Reed-frost model, the effective repoduction number at time unit \(t\) is \(\mathcal{R}_{eff} = S_{t}p\). Where \(S_{t}\) is the number of susceptible individuals.
Below, lets consider the expected number of infections for \(S_{0}\) number of susceptibles. In other words, we do not necesarrily choose to have an entirely susceptible population (\(S_{0} \approx \) N).
where \(s_{0}\) is the proportion of susceptibles and \(\text{immune}\) is the proportion of people who are immune.
The quantity \(q\) is called the Herd Immunity Threshold if, for such a value \(q\), an outbreak occurs if the proportion of susceptible individuals exceeds \(q\) and an outbreak does not occur otherwise. For the Reed-Frost Dynamical system, the Herd Immunity Threshold is \(1 - \frac{1}{\mathcal{R}_{0}}\).
Lets take a look at the effective repoduction number and herd immunity threshold below.
<function __main__.Reed_Frost_Dynamical_system(sims=10, T=15, N=1000, i0=1, R0=1, s0=999, show=True)>
The growth rate and estimating the basic reproduction number at the onset of an outbreak#
During the onset of an outbreak, then the majority of individuals are susceptible to infection, we can take advantage of the fact that the expected number of infected individuals equals
to estimate the basic reproduction number.
We can rearrange the above equation as
If we plot on the vertical axis the log of the reported number of incident cases per time unit and on the horizontal axis we plot time, then we can fit a linear regression without intercept to estimate the log of the reproduction number \(\log\left[\mathcal{R}_{0}\right]\).
Let data \(\mathcal{D} = \left\{ (t_{0}, y_{0}),(t_{1}, y_{1}),\cdots,(t_{T}, y_{T}) \right\}\) where \(t_{i}\) are time units and \(y_{i}\) are log incident cases. Then we can suppose a linear regression model
where \(\mathcal{N}(\mu,\sigma^{2})\) is the normal density with expected value \(\mu\) and variance \(\sigma^{2}\).
Because \(\beta = \log\left[\mathcal{R}_{0}\right]\) an estimate of \(\beta_{1}\) (denoted \(\hat{\beta_{1}}\)) is an estimate for \(\log\left[\mathcal{R}_{0}\right]\).
So then an estimate of \(\mathcal{R}_{0}\) is
Below, we simulate data from the Reed-Frost model and fit this line. We output a point estimate of the basic reproduction number.
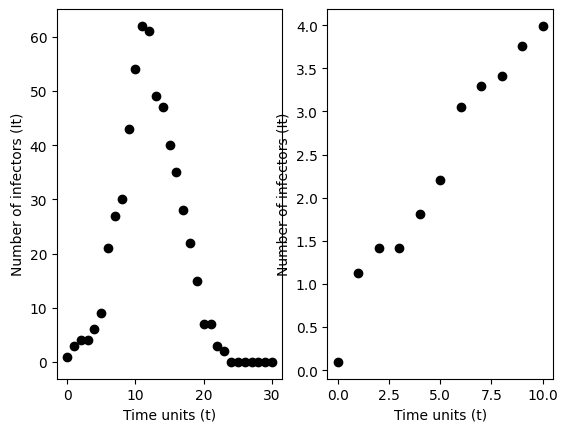
<function __main__.Reed_Frost_Dynamical_system(sims=10, T=15, N=1000, i0=1, R0=1.25, show=True)>
The ability to study epidemic chains#
Define an epidemic chain as the number of infected individuals over discrete time units. We will denote an epidemic chain as \(i^{1}-i^{2}-i^{3}-i^{4}-i^{5}-\cdots\) where \(i^{1}\) specifies the number of infected individuals within the first time unit, \(i^{2}\) specifies the number of infected within the second time units and so on.
For example, if we consider a household of 4 individuals then a feasible chain is 1-2-1 and can be read “one individual was infected. This indiviudal infected two household members, and one of these two household members (not the original infected individual) infected the last household member who was still susceptible.”. There are many possible epidemic chains for a household of four individuals. More examples include: 3- or “Three individuals were infected in one time unit and none after”; 1-1-2 or “One individual infected another and this second individal infected the remaining two individuals”.
To compute the probability of an epidemic chain, we defer to the Reed-Frost model.
If the probabiltiy of infection equals \(p=0.1\) then we can compute the above two binomial probabilities (For example, a free calculator is here = https://homepage.divms.uiowa.edu/~mbognar/applets/bin.html, and find that
Homework#
Please compute the probability of escape for a single susceptible individual given that there is a single infector and
\(p=1/10\)
\(p=1/100\)
Please compute the probability that a susceptible is infected by at least one infector given:
There are 5 infectors and \(p=1/10\)
There are 0 infectors and \(p=1/10\)
There are 2 infectors and \(p=1/20\)
An alternative to the Reed-Frost model is Greenwood’s model. For Greenwood’s, the probability of infection is equal to \(p\) and not \(1-(1-p)^I_{t}\) as it is in the Reed-Frost Dynamical System. That is, Greenwood’s model assumes exposure to two or infectors is equivalent to exposure of a single infector. In a brief 2-3 sentences, please describe when Greenwood’s model may an appropriate model of the spread of a pathogen (as opposed to the Reed-Frost model).
In the section `Dynamics assumed at start of outbreak’ we made assumptions about \(S_{0}\) and the form of \(1-(1-p)^{i_{0}}\) to arrive at an approximation solution for how an epidemic grows. To arrive at a better approximation, please recompute the dynamics at the start of an outbreak using the following, more accurate, assumptions
\(\begin{align} S_{0} &= (N-1)\\ e^{x} &\approx 1 + x + \frac{x^{2}}{2}\\ \log(1-x) &\approx -x -\frac{x^{2}}{2} \end{align}\)
Your final answer will be a more complicated expression than our original assumptions that led to \(Np\). Do you feel that the more complicated mathematical expression that you found is worth the extra computation? Why or why not?
At the start of the an outbreak, we assumed that there was a sigle infector. How do you expect the dynamics to change if there were more than one infector? Would identifying as many infectors as possible be important to public health? Using ideas from the ‘Dynamics assumed at start of outbreak’ please justify your answer.
In the section “Relationship between Reproduction number and outbreak.” we assumed that there was a single infector at the beginning of an outbreak and developed the expression \(\mathbb{E}(I_{t}) = \mathcal{R}_{0}^{t}\). Please develop a more general expression for the expected number of infectors over time of there are \(i^{0}\) infectors. In other words, if there are \(i^{0}\) infectors than \(\mathbb{E}(I_{t}) =?\)
Using your answer from (6), please plot the expected number of infectors for 5 time points, given \(p=0.1,N=100,i_{0}=1\), \(p=0.1,N=100,i_{0}=2\), and \(p=0.1,N=100,i_{0}=0\). Review these three lines: Is it more important to correctly estimate the basic reproduction number or the initial number of infectors? If there a value of the number of infectors that is important to an outbreak? Please justify your answer.
Please compute the Herd Immunity Threshold for the following scenarios
There are 5 infectors and \(\mathcal{R}_{0}=1.50\)
There are 2 infectors and \(\mathcal{R}_{0}=1.25\)
There are 3 infectors and \(\mathcal{R}_{0}=2.00\)
There are 0 infectors and \(\mathcal{R}_{0}=2.00\)
When we computed conditions for when an the number of expected infectors would increase (i.e. when an outbreak will take place) we used several assumptions: (1) the number of susceptibles is close to \(N\), (2) the probability of infection is small. Lets investigate how the conditions for an outbreak would change if we removed assumptions (1) and (2).
If we remove assumptions (1) and (2) then we can state that our new condition for an outbreak is when the expected number of infectors at time \(1\) is larger than the expected number of infectors at time zero, or
\(\begin{align} \mathbb{E}(I_{1}) = S_{0} \left[ 1- (1-p)^{i_{0}}\right] > i_{0} \end{align}\)
9.1. Please continue to solve the above inequality until there is a \(S_{0}\), alone, on the left of the inequality and then express this as the proportion of immune individuals. Note 1: We will assume that there are no removed at this stage. This means that s+i=n (This this to replace i_{0} on the right hand side). Note 2: The proportion of immune is one minus the proportion of susceptible or (imm = 1-s).
9.2. Assume that \(N=1000\), the number of infectors at time 0 equals 200, and \(p=0.002\). Will an outbreak occur? Why or why not?
9.3. Assume that \(N=1000\), the number of infectors at time 0 equals 400, and \(p=0.002\). Will an outbreak occur? Why or why not?
9.4. Based on your answers to (2) and (3) above, please comment on how the initial number of infectors may determine whether or not an outbreak occurs? Suppose you are a public health official, what do these observations mean for potential directives to the general public?
During the 2022 mpox outbreak, the Centers for Disease Control and Prevention (CDC) collected he number of incident cases of mpox and stored that data here = https://www.cdc.gov/poxvirus/mpox/response/2022/mpx-trends.html. The data for the first 100 days from 05/10/2022 to 08/16/2022 is stored on course site. Please use this data to estimate the basic reproduction number for the 2022 mpox outbreak in the US. Note: Excel can compute the needed estimate of slope.
Given, N=5 and p=0.10, please compute the probability of the following epidemic chains
1-2-1
1-0
0-1-2
2-1-1-1
End