Metapopulation models

13. Metapopulation models #

Canonical example #

The canonical example (worth studying in detail) of a metapopulation starts with the traditional SIR model and considers splitting this population into two sets: set one denoted with a subscript 1 and subscript 2. We will take the three disease states from our traditional SIR model and now assign individuals to \(S_{1}\) and \(S_{2}\); \(I_{1}\) and \(I_{2}\); and \(R_{1}\) and \(R_{2}\). An individual from population “1” in the infected disease state is assigned to the compartment \(I_{1}\) and so on.

The partition into two populations is meant to be vague because this partition could represent many different scenarios. There may be a physical barrier between the two populations that makes commuting between populations possible but difficult. Another example could be two age groups in the same location that have minimal contact with one another or are two population in which you expect that the dynamics within these groups is different than between these groups.

First we will present the canonical “two-population” metapopulation model and then discuss the assumptions in this model.

(13.1)#\[\begin{align} \frac{dS_{1}}{dt} &= -S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} + \rho \frac{I_{2}}{N_{1}} \right) \right] \\ \frac{dI_{1}}{dt} &= S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} + \rho \frac{I_{2}}{N_{1}} \right) \right] - \gamma I_{1} \\ \frac{dR_{1}}{dt} &= \gamma I_{1} \\ \\ \frac{dS_{2}}{dt} &= - S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{2}} \right) \right] \\ \frac{dI_{2}}{dt} &= S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{2}} \right) \right] - \gamma I_{2} \\ \frac{dR_{2}}{dt} &= \gamma I_{2} \\ \end{align}\]

This metapopulation model looks similar to the one-population model, except with a more complicated force of infection.

The force of infections for the one-population and two-population SIR model are

(13.2)#\[\begin{align} \lambda_{\text{one pop}} &= \beta \frac{I}{N}; \; \lambda_{\text{two pop}} = \beta \left( \frac{I_{1}}{N_{1}} + \rho \frac{I_{2}}{N_{1}} \right) \\ \end{align}\]

The force of infection for the two-population has an additional \(( \beta \rho I_{2}/N_{1} )\) term for the individuals assigned to “population one” Note that the denominator of this extra transmission term is \(N_{1}\)—the individuals who are in population one. This assumes that transmission occurs when an individual in population two commutes to population one and then contacts a susceptible in population one. In other words, transmission occurs in population one. The parameter \(\rho\) reflects the amount of interaction, often called the amount of “coupling” between the two populations. The range for this parameter is typically between zero (no interaction) up to one (full interaction).

Lets look, mathematically at the extreme case of \(\rho=0\) When \(\rho=0\) our model reduces to

(13.3)#\[\begin{align} \frac{dS_{1}}{dt} &= -S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} \right) \right] \\ \frac{dI_{1}}{dt} &= S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} \right) \right] - \gamma I_{1} \\ \frac{dR_{1}}{dt} &= \gamma I_{1} \\ \\ \frac{dS_{2}}{dt} &= - S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} \right) \right] \\ \frac{dI_{2}}{dt} &= S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} \right) \right] - \gamma I_{2} \\ \frac{dR_{2}}{dt} &= \gamma I_{2} \\ \end{align}\]

By setting \(\rho=0\) we uncouple these populations. They do not interact and because they do not interact they cannot transmit a pathogen between one another.

Simulation with no interaction and minimal interaction #

We will setup up the above metapopulation model for two scenarios. In scenario one we set \(\rho=0\) and in scenario two we set \(\rho = 0.001\). At time zero, in the first population, there is one infector and in the second population there are zero infectors.

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

def vary_rho(rho):
    def sir_two_populations(t, y, beta1, gamma, rho, N1, N2):
        S1, I1, R1, S2, I2, R2 = y
        
        dS1_dt = -S1 * beta1 * (I1 / N1 + rho * I2 / N1)
        dI1_dt =  S1 * beta1 * (I1 / N1 + rho * I2 / N1) - gamma * I1
        dR1_dt = gamma * I1
        
        dS2_dt = -S2 * beta1 * (I2 / N2 + rho * I1 / N2)
        dI2_dt = S2 * beta1 * (I2 / N2 + rho * I1 / N2) - gamma * I2
        dR2_dt = gamma * I2
        
        return [ dS1_dt, dI1_dt, dR1_dt
                ,dS2_dt, dI2_dt, dR2_dt]
    
    # Parameters
    beta1 = 0.7  # Infection rate
    gamma = 0.5  # Recovery rate
    N1, N2 = 1000, 1000  # Population sizes
    
    # Initial conditions
    S1_0, I1_0, R1_0 = N1 - 1, 1, 0  # Population 1
    S2_0, I2_0, R2_0 = N2 - 0, 0, 0  # Population 2
    y0 = [ S1_0, I1_0, R1_0
          ,S2_0, I2_0, R2_0]
    
    # Time span
    t_span = (0, 100)  # 100 days
    t_eval = np.linspace(*t_span, 1000)
    
    # Solve the system
    solution = solve_ivp(sir_two_populations
                         , t_span
                         , y0
                         , args   = (beta1, gamma, rho, N1, N2)
                         , t_eval = t_eval)
    return solution 
    

# Plot results
fig,axs = plt.subplots( 1,3, figsize=(9, 4))

ax = axs[0]
solution = vary_rho(0)
ax.plot(solution.t, solution.y[1], label='I1 (Population 1)', linestyle='dashed')
ax.plot(solution.t, solution.y[4], label='I2 (Population 2)', linestyle='dashed')

ax.set_xlabel('Time (days)')
ax.set_ylabel('Population')
ax.set_title("Rho=0")
ax.legend()


ax = axs[1]
solution = vary_rho(0.001)
ax.plot(solution.t, solution.y[1], label='I1 (Population 1)', linestyle='dashed')
ax.plot(solution.t, solution.y[4], label='I2 (Population 2)', linestyle='dashed')

ax.set_xlabel('Time (days)')
ax.set_ylabel('Population')
ax.set_title("Rho=0.001")


ax = axs[2]
solution = vary_rho(0.01)
ax.plot(solution.t, solution.y[1], label='I1 (Population 1)', linestyle='dashed')
ax.plot(solution.t, solution.y[4], label='I2 (Population 2)', linestyle='dashed')

ax.set_xlabel('Time (days)')
ax.set_ylabel('Population')
ax.set_title("Rho=0.01")

fig.set_tight_layout(True)
plt.show()

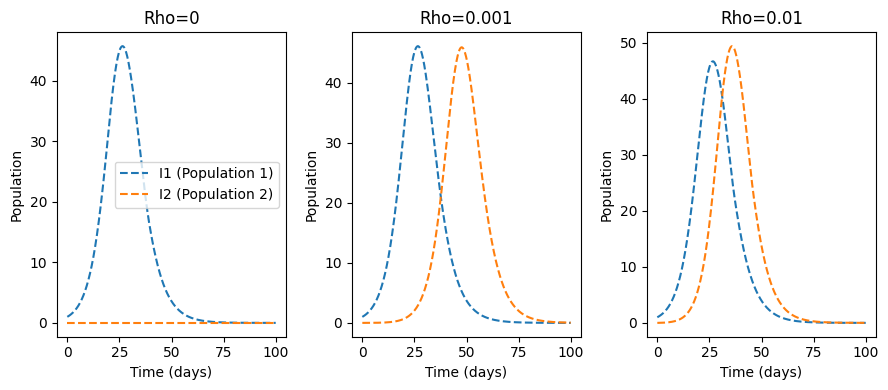
_images/f7da5c7de4a60b6176cf709d7c271b41fd2d456abafb470c8ae1c1575511a199.png

Force of infection and Strength of interaction #

Principles learned from this simulation #

Not surprisingly, in the “isolated” metapopulation model we observe that in population one the number of infections follows the typical SIR pattern. In population two, there are zero infections and no way for population one to interact with population two. This results in zero infections in population two over the observed time period.

For the “minimal interaction” model, we see that infectors in population one interact with those susceptibles in population two. This results in the beginning of an outbreak later in time than the one present in population one.

This example illustrates two principles in metapopulation models: (1) Even in a population with no infectors (zero-infector pop) an outbreak will occur. This is because infectors in the coupled population come into contact with individuals in the “zero-infector” population. (2) For populations with little or no infectors, you will observe a lag in the number of infectors compared to the population that started with infectors.

This has public health implications—it is not enough to study a population in isolation. We should work to identify other populations that our population under study come into contact with. Infections in those other populations modulate the probability of an outbreak in our population of study.

Example of dynamics #

Starting an epidemic in a neighboring area #

Probability of an epidemic #

Movement and commuting example #

Extinction and coupling #

Mathematical demonstration of the above principles #

The treatment below follows closely the work by Keeling and Rohani.

We can also demonstrate the above principles using mathematics. Lets assume that we are early in the outbreak for population one—before many, if at all any, infectors come into contact with population two. Remember for this setting, population two has no initial infectors.

Then the change in the number of infectors for population two equals

(13.4)#\[\begin{align} \frac{dI_{2}}{dt} &= S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{2}} \right) \right] - \gamma I_{2} \\ & = N_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{2}} \right) \right] - \gamma I_{2} \;\; \text{(Beginning of outbreak)} \\ & = \beta_{1} \left( I_{2} + \rho I_{1} \right) - \gamma I_{2} \\ &= \left(\beta_{1} - \gamma\right) I_{2} + \beta_{1} \rho I_{1}\\ \frac{dI_{2}}{dt} - \left(\beta_{1} - \gamma\right) I_{2} &= \beta_{1} \rho I_{1} \end{align} \]

If we can solve the above equation then we would arrive at a function \(I_{2}(t)\) of the number of infectors in population two over time. This function could describe the factors influencing \(I_{2}\). We can already understand some of the factors influencing \(I_{2}\). We see that the number of infectors in population two depends on the: (1) the number of infectors in population one and (2) the amount of “coupling”. This is because of the term \(\beta_{1} \rho I_{1}\) on the right hand side of this differential equation.

Is there a reasonable way to arrive at an \(I_{2}(t)\)?

Mathematical aside (Integrating factors)#

The majority of analytical solutions to differential equations fall into two categories: (1) good guesses and (2) placing our differential equation into a specific form that we know has a general solution. Integrating factors are of solution type (2).

Form calculus, the product rule states that, given two functions \(f(t)\) and \(g(t)\),

(13.5)#\[\begin{align} \left[ f(t)g(t) \right]' = f'(t)g(t) + f(t)g'(t) \end{align}\]

When we look at the left hand side of our differential equation, we see it looks close to the result of the product rule

(13.6)#\[\begin{align} I_{2}'(t) - \left(\beta_{1} - \gamma\right) I_{2} \\ \end{align}\]

We just need a “g” function multiplied by \(I_{2}'(t)\). Lets just add this and see where we get.

We will suppose there exists some function \(g(t)\) and multiply left and right by this function

(13.7)#\[\begin{align} g(t)I_{2}'(t) - g(t)\left(\beta_{1} - \gamma\right) I_{2} &= g(t)\beta_{1} \rho I_{1} \end{align}\]

Well what if the left hand side really was the result of \(\left[I_{2}(t)g(t)\right]'\)?

Then

(13.8)#\[\begin{align} \left[I_{2}(t)g(t)\right]' &= g(t)\beta_{1} \rho I_{1} \\ I_{2}(t)g(t) &= \int g(t)\beta_{1} \rho I_{1} \; dt + C \\ I_{2} (t) &= \frac{1}{g(t)} \left[ \int g(t)\beta_{1} \rho I_{1} \; dt + C \right] \end{align}\]

In other words, if the left hand side of our differential equation really is \(\left[I_{2}(t)g(t)\right]'\) then we can solve for \(I_{2}(t)\). Well what does this imply?

(13.9)#\[\begin{align} \left[I_{2}(t)g(t)\right]' &= g(t)I_{2}'(t) - g(t)\left(\beta_{1} - \gamma\right) I_{2} \\ I_{2}(t)g'(t) &= - I_{2}(t) g(t)\left(\beta_{1} - \gamma\right) \\ g'(t) &= -g(t)\left(\beta_{1} - \gamma\right) \\ \end{align}\]

We know how to solve the above diffeq. This is just \(g(t) = e^{ -t(\beta_{1} - \gamma) }\)

Then our final solution is

(13.10)#\[\begin{align} I_{2} (t) &= \frac{1}{g(t)} \left[\int g(t)\beta_{1} \rho I_{1} \; dt + C \right] \\ I_{2} (t) &= e^{ t(\beta_{1} - \gamma)} \left[\int_{0}^{t} e^{ -t(\beta_{1} - \gamma)}\beta_{1} \rho I_{1}(t) \; dt + C \right] \end{align}\]

We can solve for \(C\) by setting time to zero

(13.11)#\[\begin{align} I_{2} (0) &= e^{ t(\beta_{1} - \gamma)} \left[\int_{0}^{t} e^{ -t(\beta_{1} - \gamma)}\beta_{1} \rho I_{1}(t) \; dt + C \right] \\ I_{2} (0) &= C \implies \\ I_{2} (t) &= e^{ t(\beta_{1} - \gamma)} \left[\int_{0}^{t} e^{ -t(\beta_{1} - \gamma)}\beta_{1} \rho I_{1}(t) \; dt + I_{2}(0) \right] \\ \end{align}\]

We see, a few key principles from this analysis. The growth of growth of infectors in population two depends on the number of infectors in population two and the number of infectors in population one. We see also that the rate of growth of infectors in population two is exponential, depending on the coupling between population one and two; and on the transmission and infectious periods. When \(\rho=0\) our growth reduces to the simple “one population SIR”.

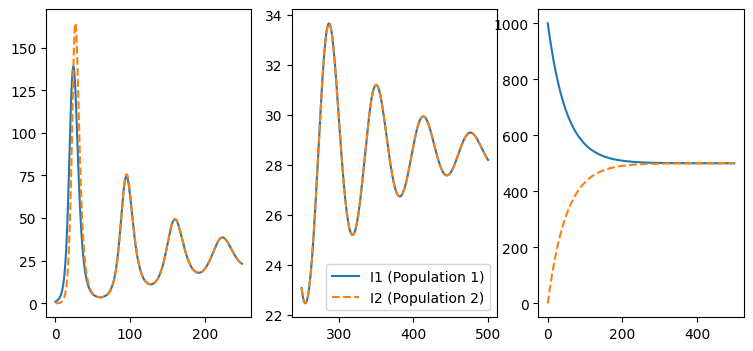
A more principled look at “strength of interaction”#

import numpy as np
from scipy.integrate import solve_ivp
import matplotlib.pyplot as plt

def vary_rho(rho):
    def sir_two_populations(t, y, beta, gamma, come_home, go_away,mu):
        Sxx,Sxy,Syx,Syy,Ixx,Ixy,Iyx,Iyy,Nxx,Nxy,Nyx,Nyy = y
        
        dSxx_dt = mu*Nxx-beta * Sxx * (Ixx + Iyx)/( Nxx + Nyx ) + come_home*Sxy - go_away*Sxx
        dSxy_dt = mu*Nxy-beta * Sxy * (Iyy + Ixy)/( Nyy + Nxy ) - come_home*Sxy + go_away*Sxx
        
        dSyx_dt = mu*Nyx-beta * Syx * (Ixx + Iyx)/( Nxx + Nyx ) - come_home*Syx + go_away*Syy
        dSyy_dt = mu*Nyy-beta * Syy * (Iyy + Ixy)/( Nyy + Nxy ) + come_home*Syx - go_away*Syy

        dIxx_dt = beta * Sxx * (Ixx + Iyx)/( Nxx + Nyx ) + come_home*Ixy - go_away*Ixx - gamma*Ixx
        dIxy_dt = beta * Sxy * (Iyy + Ixy)/( Nyy + Nxy ) - come_home*Ixy + go_away*Ixx - gamma*Ixy
        
        dIyx_dt = beta * Syx * (Ixx + Iyx)/( Nxx + Nyx ) - come_home*Iyx + go_away*Iyy - gamma*Iyx
        dIyy_dt = beta * Syy * (Iyy + Ixy)/( Nyy + Nxy ) + come_home*Iyx - go_away*Iyy - gamma*Iyy

        dNxx_dt    = come_home * Nxy - go_away * Nxx
        dNyy_dt    = come_home * Nyx - go_away * Nyy

        dNxy_dt    = -come_home * Nxy + go_away * Nxx
        dNyx_dt    = -come_home * Nyx + go_away * Nyy
        
        return [ dSxx_dt, dSxy_dt, dSyx_dt, dSyy_dt
               , dIxx_dt, dIxy_dt, dIyx_dt, dIyy_dt
               , dNxx_dt, dNxy_dt, dNyx_dt, dNyy_dt] 
    
    # Parameters
    beta      = 0.7  # Infection rate
    gamma     = 0.5  # Recovery rate
    mu        = 1./70
    
    come_home = 0.01
    go_away   = 0.01

    Nxx, Nyy = 1000, 1000  # Population sizes
    Nxy, Nyx = 0, 0 # Population sizes

    # Initial conditions
    Sxx,Sxy,Syx,Syy = 999,0,0,1000
    Ixx,Ixy,Iyx,Iyy = 1,0,0,0

    y0 = [Sxx,Sxy,Syx,Syy,Ixx,Ixy,Iyx,Iyy,Nxx,Nxy,Nyx,Nyy]
    
    # Time span
    t_span = (0, 500)  # 100 days
    t_eval = np.linspace(*t_span, (t_span[-1]-t_span[0])*2 )
    
    # Solve the system
    solution = solve_ivp(sir_two_populations
                         , t_span
                         , y0
                         , args   = (beta, gamma, come_home, go_away,mu)
                         , t_eval = t_eval)
    return solution 
    

# Plot results
fig,axs = plt.subplots( 1,3, figsize=(9, 4))

solution = vary_rho(0)

ax = axs[0]
Ix = solution.y[4] + solution.y[5]
Iy = solution.y[6] + solution.y[7]

ax.plot(solution.t[:500:], Ix[:500] , label='I1 (Population 1)')
ax.plot(solution.t[:500], Iy[:500],  label='I2 (Population 2)', linestyle='dashed')

ax = axs[1]
ax.plot(solution.t[-500:], Ix[-500:] , label='I1 (Population 1)')
ax.plot(solution.t[-500:], Iy[-500:],  label='I2 (Population 2)', linestyle='dashed')

ax.legend()

ax = axs[2]

Nxx = solution.y[-4]
Nxy = solution.y[-3]
Nyx = solution.y[-2]
Nyy = solution.y[-1]

ax.plot(solution.t, Nxx , label='I1 (Population 1)')
ax.plot(solution.t, Nyx,  label='I2 (Population 2)', linestyle='dashed')

[<matplotlib.lines.Line2D at 0x7f58b790ca50>]

_images/cd05ee5e6debe6f52d1049463eaa8a71ad8041356e18a3b1636c25c6bfc16ac5.png

Homework #

Build a metapopulation model with three populations that follow SEIR dynamics (with vital dynamics). This metapopulation model should be the first type that we studied that included the parameter \(\rho\) for “coupling strength”.
We will consider the transmission rate to be the same between all populations and equal to \(\beta = 1.0\), the rate of movement from exposed to infectious to be the same \(\sigma = 1/10\), and the rate of movement from infectious to removed to be the same \(\gamma=0.7\). The first population has \(N=1000\), second population \(N=500\), and third population \(N=100\) individuals. The third population \((M=100)\) has a single infected. The other two populations only have susceptible individuals. The “strength of interaction between the three populations is 0.05.
1. Run the above model for 300 time units. Plot the infected for populations one, two, and three.
2. Run three iterations of the model:
  1. The first pop has a single infector and everyone else is susceptible
  2. The second pop has a single infector and everyone else is susceptible
  3. The third pop has a single infector and everyone else is susceptible
3. For each of the three scenarios above, please plot the number of infectors over time (add a legend).
4. For each scenario, please record the sum of the total number of individuals in the removed category for each population. Those who are in the removed category have gone through the infectious process. They were exposed and infected at some point. What scenario has the largest number of removed individuals? Why? Can you provide a rationale for someone who doesnt understand metapopulation models and for someone who does?
Integrating factor Consider the following metapopulation model

(13.12)#\[\begin{align} \frac{dS_{1}}{dt} &= -S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} + \rho \frac{I_{2}}{N_{2}} \right) \right] \\ \frac{dI_{1}}{dt} &= S_{1} \left[ \beta_{1} \left( \frac{I_{1}}{N_{1}} + \rho \frac{I_{2}}{N_{2}} \right) \right] - \gamma I_{1} \\ \frac{dR_{1}}{dt} &= \gamma I_{1} \\ \\ \frac{dS_{2}}{dt} &= - S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{1}} \right) \right] \\ \frac{dI_{2}}{dt} &= S_{2} \left[ \beta_{1} \left( \frac{I_{2}}{N_{2}} + \rho \frac{I_{1}}{N_{1}} \right) \right] - \gamma I_{2} \\ \frac{dR_{2}}{dt} &= \gamma I_{2} \\ \end{align}\]

and note that this metapopulation considers two types of infections: susceptibles in their “home” population can be infected by infectors in their home population OR susceptibles who travel to the second population can be infected by individuals in that second population.

This is different than the first model we explore in the notes. In the notes we considered “home infection” and infection by those who commute to the susceptible’s home population.

Please use the integrating factor approach that was discussed in class to derive a solution to \(I_{2}(t)\). This solution will look very similar to the notes except for one key difference. Please discuss the factors that influence \(I_{2}\). What additional factor influences \(I_{2}\) in this model that we did not see in the model presented in class. Why does this factor matter for this model and not for the model presented in class?

Interventions In our previous “one population” modeling framework we could only explore interventions that reduced the transmission rate. To model isolation or quarantine, we needed to reason that deploying these types of interventions would map to some suitable reduction in transmission rate. With a metapopulation framework, we can explore, closer, the impact of quarantine/isolation on the number of infectors over time.
1. Given the “more principled” metapop model, how would we model isolating one group from another and why?
2. As public health practitioners, we expect that an isolation mandate may not be totally adhered to. In other words, if we quarantine one population from another then not everyone will comply. Given the principles we learned about metapop models so far, would a minor number of non-adherant residents still continuing to contact others prevent an outbreak?

Metapopulation models

Contents

Mathematical aside (Integrating factors)#